RaysWebClass.Com - Computer Basics
[ Computer Components | Binary | Bytes | Hexadecimal | Data Packet | ASCII | myIP ]


Computer Components

All computers can be divided into four parts:


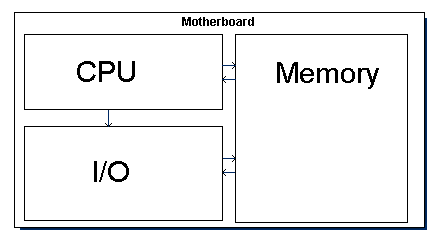
Motherboard
A thin block of plastic wired to accommodate a CPU, Memory, and I/O devices.
(view a picture of a Motherboard)

CPU - Central Processing Unit
The CPU (Central Processing Unit) is sometimes referred to as the "brain" of the computer - computer - the component that does all the work. It makes decisions, runs programmes, and transfers information to and from Memory and I/O.
Memory - The place where data and programmes are stored
Memory is divided into small blocks called bytes (see below). The The CPU (Central Processing Unit) is sometimes referred to as the "brain" of the computer - the component that does all the work. It makes decisions, runs programmes, and transfers information to and from Memory and I/O. Memory – The "Space" designed to store data and programmes. Memory is divided into small blocks called bytes (see below). The CPU stores and retrieves information by “bytes.” Each byte has an address (a way to find it) and storage capacity (where it can store a small amount of information, like the letter "A" for instance). The CPU can either Read or Write information to a byte. For example, a programmer may write the line X = 9. The CPU would looks for, and finds an unused location of memory (e.g. 1011) and stores the number 9 there. This is called writing to memory.) The next time the programmer needs this information he/she may write the line Response.Write X. The CPU will go back to the memory location (1011), retrieve the data and display it. This is called reading from memory. The user of the program will simple see 9 on the screen.

There are two types of memory in a computer. They are RAM (random access memory). This is the type of memory we've been talking about. The other type is the ROM (read only memory). This memory contains the computer’s permanent data. RAM requires power to keep retain data, whereas, ROM does not. Important!

Before turning off your computer you may want to copy your data to the hard drive so you will not lose it. Copying data to the hard drive is called saving data or just save. Memory come is 'sticks.' *You may want to Look up 'memory stick' to see how much memory the stick contains and, how much it costs.
The Input/Output (IO) devices

Input/Output refers to all the other devices that are part of your computer. These include the Monitor, Keyboard, Hard Drives, CD ROMs, DVD's Printers, etc. All are I/O devices. Some for these devices, such as Monitors, Printers are used only for outout. Others, such as the Keyboards, CD ROMs are used only for input. And still others can do both, such as Hard Drives, Read/Write CD’s and Read/Write DVD’s. Devices that store information outside memory are sometimes called Secondary Memory Devices, such as the Hard Drive. Electronic computer are fast and cheep, but they have one serious drawback. If they lose power, even for a second, they will lose information from memory. If you have ever worked on a document for hours, then lost all for your work because of a computer froze-up (usually due to power fluctuations), you know what I mean! By saving information frequently to the Hard Drive, CD, or DVD, you can avoid losing too much work if the power goes out. Spintronic computers may solve this problem, but there not out on the market yet.

One way to avoid data loss from sudden power failures is to purchase a battery backup (UPS – uninterruptable power supply) system. They’re usually inexpensive and can save your nervous system from crashing as well. Such a system will keep your computer power on from 15 to 20 minutes – providing enough time to back up your data and safely turn off your computer until the power returns.

You may notice that information flows from the CPU to memory and from memory to the I/O devices freely, but not from I/O to the CPU. The CPU controls which I/O devices are working and where. In memory, information is being received or sent, but it does not interact with raw information coming from these I/O devices.
The Power Supply
The Computers Power Supply could be considered a fifth division. Without power the computer is useless. However the power supply does not contribute to data storage or transfer so it’s usually not included on the list.

Binary Numerical System

A digital computers is a binary bits. That is, each bit of information saved in the computer is save in binary format. The binary number system is very different from the decimal system we use every day. First, binary numbers have only two digits: 0 (zero) and 1 (one). The following chart shows how you would count from 0 (zero) to 15 (fifteen) in both systems:

Binary Decimal
0 0
1 1
10 2
11 3
100 4
101 5
110 6
111 7
1000 8
1001 9
1010 10
1011 11
1100 12
1101 13
1110 14
1111 15

So, the number 5, in a computer will be stored as 101.
Binary Math:

1001
+ 110
1111


1001 (9) + 110 (6) = 1111 (15). This Binary math looks the same as decimal, but look at this one:

1
+ 1
10


This example is less obvious, your instenct is to say the answer is 2, but there is no 2 in binary.
1 + 1 is 10, or "0 carry 1." eg:

11
+ 11
110


1 + 1 + 1 = 11. You may ask, why go through all this trouble? Why not just make computers decimal? It's the simplicity of the binary computer that makes it so appealing and cheep! Binary numbers can be represented in a computer as an open or closed circuit. An open circuit is 0 and a closed circuit is 1.



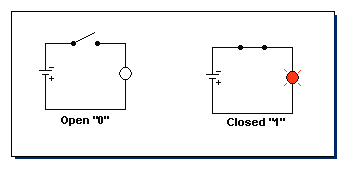
This is the simplest circuit, we know, and when you need to make billions of them, it's the cheepest too! Converting binary to decimal and back again is a well known technique. All computers are "born" knowing how to do it. Let's say, for example, we want to add 248 and 182. The computer would have to first, convert these numbers to binary. You will do this by dividing powers of 2.

20 = 1
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
29 = 1024
210 = 2048


Let's start with the first number 248. The largest power of two to go into 248 is 27.

(27 ) 128 ÷ 248 = 1 R 120   (1 time with a Remainder of 120)
(26 ) 64 ÷ 120 = 1 R 56
(25 ) 32 ÷ 56 = 1 R 24
(24 ) 16 ÷ 24 = 1 R 8
(23 ) 8 ÷ 8 = 1 R 0
(22 ) 4 ÷ 0 = 0 R 0
(21 ) 2 ÷ 0 = 0 R 0
(20 ) 1 ÷ 0 = 0 R 0


Result: 11111000

And the second number 182:

(27) 128 ÷ 182 = 1 R 54
(26) 64 ÷ 54 = 0 R 54
(25) 32 ÷ 54 = 1 R 22
(24) 16 ÷ 22 = 1 R 6
(23) 8 ÷ 6 = 0 R 6
(22) 4 ÷ 6 = 1 R 2
(21) 2 ÷ 2 = 1 R 0
(20) 1 ÷ 0 = 0 R 0


Result: 10110110

11111000
+ 10110110
110101110


Now we need to convert back to decimal and add.

1*28 + 1*27 + 0*26 + 1*25 + 0*24 + 1*23 + 1*22 + 1*21 + 0*20 =
256 + 128 + 0 + 32 + 0 + 8 + 4 + 2 + 0 = 430


Digital computers make these conversions millions of times a second.

The Byte

A byte is 8 bits. A bit is a 0 or a 1. Each bit is an open or closed circuit. Each byte can have 256 different combinations of 1s and 0s:

0 0 0 0 0 0 0 0
= 0
0 0 0 0 0 0 0 1
= 1
0 0 0 0 0 0 1 0
= 2
0 0 0 0 0 0 1 1
= 3
0 0 0 0 0 1 0 0
= 4
0 0 0 0 0 1 0 1
= 5
0 0 0 0 0 1 1 0
= 6
0 0 0 0 0 1 1 1
= 7
0 0 0 0 1 0 0 0
= 8
.
.
.
1 1 1 1 1 1 0 0
= 252
1 1 1 1 1 1 0 1
= 253
1 1 1 1 1 1 1 0
= 254
1 1 1 1 1 1 1 1
= 255


ASP uses the following variable size chart:

Data type

Storage size

Range

Byte

1 byte

0 to 255

Integer

2 bytes

-32,768 to 32,767

Long (Integer)

4 bytes

-2,147,483,648 to 2,147,483,647

Single (floating)

4 bytes

-1.401298E-45 to 3.402823E38

Double (floating)

8 bytes

-4.94065645841247E-324 to 1.79769313486232E308



1 bit = 0 or 1
1 byte = 8 bits
1 Kilobyte = 1024 bytes (1K)
1 Megabyte = 1024 Kilobytes (1,048,576 bytes) (millions)
1 Gigabyte = 1024 Megabytes (1,073,741,824 bytes) (billions)
1 Terabyte = 1024 Gigabytes (1,099,511,627,776 bytes) (trillions)
1 Petabyte = 1024 Terabytes (1,125,899,906,842,624 bytes) (quadrillions)
1 Exabyte = 1024 Petabytes (1018 bytes) (quintillions)
hexillion, septillion, octillion, etc.

Hexadecimal

The hexadecimal number system (or Hex for short) has 16 digits before 10:

digit Hex Dec
1st 0 0
2nd 1 1
3rd 2 2
4th 3 3
5th 4 4
6th 5 5
7th 6 6
8th 7 7
9th 8 8
10th 9 9
11th A 10
12th B 11
13th C 12
14th D 13
15th E 14
16th F 15
  10 16

To count to 100 (256 decimal) would look like this:

1 2 3 4 5 6 7 8 9 A B C D E F 10
11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 20
21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F 30
31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F 40
41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F 50
51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F 60
61 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F 70
71 72 73 74 75 76 77 78 79 7A 7B 7C 7D 7E 7F 80
81 82 83 84 85 86 87 88 89 8A 8B 8C 8D 8E 8F 90
91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F A0
A1 A2 A3 A4 A5 A6 A7 A8 A9 AA AB AC AD AE AF B0
B1 B2 B3 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF C0
C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF D0
D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF E0
E1 E2 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF F0
F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF 100


Why is this even used in computer? Well, for two reasons, one it's a lot harder to make a mistake, and two, it has direct conversion to binary:

Hex Binary
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
A 1010
B 1011
C 1100
D 1101
E 1110
F 1111

This is all you need to know! For example:

C5 in hex is 11000101 in binary.
That is C (1100) 5 (0101) = 11000101.

And 10100110 binary is A6 hex.
That is 10100110 = A6.

Converting from Hex to Decimal and back is similar to binary:

160 = 1
161 = 16
162 = 256
163 = 4096
164 = 65536
165 = 1048576
166 = 16777216


9165 in hex is:

(163) 4096 ÷ 9165 = 2 R 973
(162) 256 ÷ 973 = 3 R 205
(161) 16 ÷ 205 = 12 R 13
(160) 1 ÷ 13 = 13 R 0


Result: 23CD   (Remember 12 is C in hex and 13 is D)

1AF8 in decimal is:

1*163 + A*162   + F*161 + 8*160   =
4096  + 10*256 + 15*16 + 8*1 =
4096  +  2560    +  240    +  8   =

Result: 6904

Internet Data Packer

Internet Data Packet
return IP request IP Port part of Parity TTL Data
130.39.221.110 204.71.200.74 :80 5 23 FF01 15 0100110100100...

ASCII
ASCII stands for American Standard Code for Information Interchange. Computers can only understand numbers, so an ASCII code is the numerical representation of a character such as 'a' or '@' or an action of some sort (carriage return). ASCII was developed in the early 1960's and now, the non-printing characters are rarely used for their original purpose. (Click here to see the ASCII table). ASCII was actually designed for use with teletypes and so the descriptions are somewhat obscure. If someone says they want your data however in ASCII format, all this means is that they want 'plain text' with no formatting such as tabs, bold or underscoring - the raw format that any computer can understand. This is usually so they can easily import the file into their own applications without issues. HTML is written in plain text. Notepad creates plain text or ASCII. These days a modern browsers uses a two byte character set with 65535 - knows as entities.

My IP
This computer`s IP Address is: 66.248.200.19